#Model constructor
class HigherOrderNamingGame():
def __init__(self, simplices, rule):
#Structure
self.simplices = simplices
self.nodes = list({node for simplex in simplices for node in simplex})
self.N = len(self.nodes)
#Time
self.t = 0
#Rule
self.rule = rule
def SetInitialConditions(self, beta, p, n_A, verbose=False):
#Game parameters
self.beta = beta
self.p = p
#Opinions of the nodes (vocabularies)
self.opinions = {}
#Generating committed agents
N_p = int(self.N*self.p) #number of committed agents
#Randomly picking N_p committed agents
committed = random.sample(self.nodes, N_p)
#Setting up a committed dictionary
#self.is_committed = {n:False for n in self.nodes}
for n in self.nodes:
if n in committed:
#self.is_committed[n]=True
#Assigning opinion "A" to committed agents
self.opinions[n]=frozenset(["A"])
#Calculating the number of agents holding n_A (not committed) from the density in input
N_A = int(self.N*n_A)
N_B = self.N-N_A-N_p
#Creating a list of opinions to assign
opinions_to_assign = ['A']*N_A + ['B']*N_B
#Shuffling them
random.shuffle(opinions_to_assign)
#Agents left to be matched with opinions
noncommitted = set(self.nodes) - set(committed)
for n, o in zip(noncommitted, opinions_to_assign):
self.opinions[n]=set(o)
if verbose: print('Setup Done.', self.N, 'nodes,', "N_A:", N_A, "N_B:", N_B, "N_p:", N_p)
def AgreeOnSimplex(self, simplex, said_word):
#Updating the simplex on the agreed word
for n in simplex:
try: #There are also committed minorities which have frozensets!
self.opinions[n].clear()
self.opinions[n].add(said_word)
except AttributeError: #It was committed
pass
def ListenersLearnWord(self, listeners, said_word):
#Looping through the listeners
for listener in listeners:
try: #Trying to learn...
self.opinions[listener].add(said_word)
except AttributeError: #It was committed
pass
def play_on_simplex(self, simplex):
#Selecting speaker and listeners at random
random.shuffle(simplex)
speaker = simplex[0]
listeners = simplex[1:]
#Selecting a random word to be said
said_word = random.choice(list(self.opinions[speaker]))
words_of_listeners = [self.opinions[listener] for listener in listeners]
#Using the rule to get the words of listeners to be used for the agreement
if self.rule=='union':
words_of_listeners_by_rule = set.union(*[set(w) for w in words_of_listeners])
elif self.rule=='intersection':
words_of_listeners_by_rule = set.intersection(*[set(w) for w in words_of_listeners])
#Trying to agree based on the rule and the communication efficiency beta
if (said_word in words_of_listeners_by_rule) and (random.random() <= self.beta):
self.AgreeOnSimplex(simplex, said_word)
else: #No agreement, but the said word is learned by the listeners
self.ListenersLearnWord(listeners, said_word)
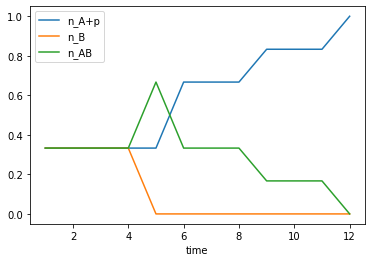
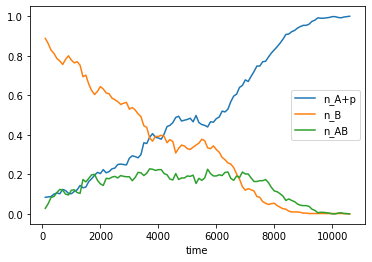
def get_densities(self):
single_opinion_counter = collections.Counter([list(opinions)[0] for opinions in self.opinions.values() if len(opinions)==1])
n_Ap = single_opinion_counter["A"]/self.N
n_B = single_opinion_counter["B"]/self.N
n_AB = 1-n_Ap-n_B
return n_Ap, n_B, n_AB
def run(self, path, t_max=100, check_every=10, print_every=1):
self.t_max = t_max
#Opening file to save densities results
densities_path = path + 'HONG_densities_N%i_beta%.4f_p%.2f.csv'%(self.N, self.beta, self.p)
f = open(densities_path,'w')
f.write('time,n_A+p,n_B,n_AB\n')
while self.t <= self.t_max:
self.t += 1
if self.t%print_every==0: print('t=%i'%self.t)
######### THIS IS FOR PLAYING ALWAYS ON ALL SIMPLICES AT EACH TIME #########
#Reshuffling the sequence of simplices
#random.shuffle(self.simplices)
#Looping over each simplex and playing
#for simplex in self.simplices:
#self.play_on_simplex(simplex)
############################################################################
#Playing on a random simplex
simplex = random.choice(self.simplices)
self.play_on_simplex(simplex)
#Storing the values every check_every time steps:
if self.t%check_every==0:
n_Ap, n_B, n_AB = self.get_densities()
line = "%i,%.3f,%.3f,%.3f\n"%(self.t, n_Ap, n_B, n_AB)
f.write(line)
#Also checking if we reached the absorbing state:
if n_Ap==1 or n_B==1:
f.close()
print('DONE! Reached the absorbing state.')
return None
f.close()
print('DONE! Run out of time...')