10. Epidemics on networks

We use the Python library “Epidemics on Networks” developed by Kiss, Miller & Simon.

The library must be installed using pip:

pip install EoN

The library documentation is available here.

import EoN
import networkx as nx
import numpy as np
from collections import defaultdict
import pandas as pd
import seaborn as sns
import matplotlib.ticker as ticker

Matplotlib is building the font cache; this may take a moment.

%pylab inline

Populating the interactive namespace from numpy and matplotlib

10.1. Epidemic threshold for homogeneous networks

We simulate the spread of an SIR on an Erdos-Renyi graph with constant recovery rate.

N = 10000
p = 0.002
G = nx.fast_gnp_random_graph(N, p)

nx.is_connected(G)

True

print(nx.info(G))

Name: 
Type: Graph
Number of nodes: 10000
Number of edges: 99584
Average degree:  19.9168

---

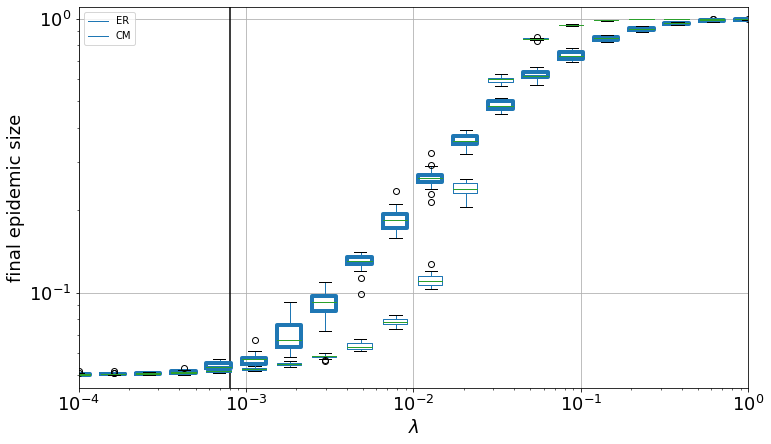
For this network the epidemic threshold can be approximated as \(\lambda_c = \frac{\mu}{\langle k \rangle}\)

mu = 0.2

avg_deg1 = 2 * len(G.edges) / N
lc = mu / avg_deg1
print(lc)

0.01004177377892031

As expected for this network, we have \(\langle k^2 \rangle \sim \langle k \rangle^2 + \langle k \rangle\)

sum_k2 = 0
for i in G.nodes():

    k = G.degree(i)
    sum_k2 += k * k

avg_k2 = sum_k2 / N
print(avg_k2)

416.0806

avg_deg1**2 + avg_deg1

416.59572224

10.1.1. Simulations of an SIR process

We simulate 20 realizations of a SIR model for increasing values of \(\lambda\) using the fast_SIR function of EoN

final_size = defaultdict(list)

for lambd in np.geomspace(0.0001, 1.0, 20):

    for r in range(0, 20):

        t, S, I, R = EoN.fast_SIR(G, lambd, mu, rho=0.05)

        final_size[lambd].append(R[-1] / N)

homo_net_size = pd.DataFrame.from_dict(final_size)

homo_net_size

	0.000100	0.000162	0.000264	0.000428	0.000695	0.001129	0.001833	0.002976	0.004833	0.007848	0.012743	0.020691	0.033598	0.054556	0.088587	0.143845	0.233572	0.379269	0.615848	1.000000
0	0.0506	0.0514	0.0516	0.0515	0.0524	0.0572	0.0608	0.0700	0.0835	0.1400	0.4589	0.7949	0.9320	0.9829	0.9971	0.9997	1.0000	1.0	1.0	1.0
1	0.0501	0.0506	0.0514	0.0523	0.0541	0.0548	0.0602	0.0684	0.0938	0.1752	0.4232	0.7858	0.9344	0.9848	0.9981	0.9996	0.9998	1.0	1.0	1.0
2	0.0506	0.0506	0.0514	0.0521	0.0548	0.0552	0.0614	0.0706	0.0855	0.1488	0.3979	0.7824	0.9336	0.9858	0.9986	0.9999	1.0000	1.0	1.0	1.0
3	0.0506	0.0507	0.0506	0.0523	0.0537	0.0569	0.0601	0.0684	0.0861	0.1429	0.4395	0.7813	0.9360	0.9852	0.9982	0.9999	1.0000	1.0	1.0	1.0
4	0.0502	0.0510	0.0518	0.0526	0.0536	0.0557	0.0609	0.0654	0.0922	0.1438	0.4822	0.7811	0.9369	0.9870	0.9981	0.9997	1.0000	1.0	1.0	1.0
5	0.0507	0.0512	0.0508	0.0516	0.0532	0.0562	0.0593	0.0718	0.0867	0.1415	0.4270	0.7792	0.9354	0.9873	0.9978	0.9999	1.0000	1.0	1.0	1.0
6	0.0505	0.0507	0.0514	0.0522	0.0538	0.0563	0.0604	0.0672	0.0921	0.1496	0.3933	0.7787	0.9303	0.9867	0.9977	0.9998	0.9999	1.0	1.0	1.0
7	0.0508	0.0507	0.0513	0.0523	0.0535	0.0561	0.0593	0.0700	0.0932	0.1549	0.4483	0.7800	0.9315	0.9858	0.9982	0.9998	1.0000	1.0	1.0	1.0
8	0.0506	0.0506	0.0516	0.0516	0.0542	0.0554	0.0613	0.0690	0.0890	0.1517	0.4168	0.7916	0.9378	0.9857	0.9983	1.0000	1.0000	1.0	1.0	1.0
9	0.0501	0.0504	0.0508	0.0519	0.0537	0.0551	0.0608	0.0674	0.1011	0.1304	0.4228	0.7800	0.9312	0.9867	0.9980	0.9999	0.9999	1.0	1.0	1.0
10	0.0506	0.0508	0.0511	0.0511	0.0538	0.0568	0.0608	0.0692	0.0893	0.1460	0.4395	0.7839	0.9300	0.9846	0.9976	0.9998	1.0000	1.0	1.0	1.0
11	0.0510	0.0506	0.0514	0.0515	0.0537	0.0558	0.0593	0.0673	0.0869	0.1531	0.4438	0.7776	0.9413	0.9843	0.9977	0.9996	1.0000	1.0	1.0	1.0
12	0.0503	0.0503	0.0511	0.0522	0.0541	0.0562	0.0616	0.0685	0.0913	0.1496	0.4670	0.7850	0.9379	0.9842	0.9972	0.9998	1.0000	1.0	1.0	1.0
13	0.0501	0.0508	0.0511	0.0517	0.0537	0.0544	0.0612	0.0688	0.0858	0.1660	0.4371	0.7954	0.9359	0.9874	0.9981	0.9995	0.9999	1.0	1.0	1.0
14	0.0503	0.0507	0.0509	0.0523	0.0549	0.0560	0.0587	0.0712	0.0856	0.1583	0.4135	0.7881	0.9309	0.9842	0.9983	0.9996	1.0000	1.0	1.0	1.0
15	0.0505	0.0505	0.0517	0.0517	0.0544	0.0567	0.0619	0.0701	0.0880	0.1548	0.4127	0.7682	0.9292	0.9872	0.9977	0.9999	0.9999	1.0	1.0	1.0
16	0.0506	0.0506	0.0509	0.0519	0.0539	0.0569	0.0589	0.0660	0.0886	0.1670	0.4257	0.7781	0.9356	0.9859	0.9981	0.9998	1.0000	1.0	1.0	1.0
17	0.0500	0.0507	0.0514	0.0525	0.0519	0.0572	0.0613	0.0689	0.0939	0.1540	0.4175	0.7905	0.9329	0.9841	0.9975	0.9995	1.0000	1.0	1.0	1.0
18	0.0503	0.0506	0.0507	0.0525	0.0525	0.0572	0.0597	0.0689	0.0831	0.1522	0.4397	0.7770	0.9420	0.9841	0.9971	0.9997	1.0000	1.0	1.0	1.0
19	0.0506	0.0516	0.0508	0.0518	0.0529	0.0564	0.0604	0.0703	0.0853	0.1463	0.4229	0.7737	0.9395	0.9861	0.9986	0.9998	1.0000	1.0	1.0	1.0

plt.figure(figsize=(12, 7))

homo_net_size.boxplot(
    positions=np.array(homo_net_size.columns),
    widths=np.array(homo_net_size.columns) / 3,
)

plt.vlines(x=lc, ymin=0.045, ymax=1.1)

plt.xscale("log")
plt.yscale("log")
plt.xlim(0.0001, 1.0)
plt.ylim(0.045, 1.1)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.ylabel("final epidemic size", fontsize=18)
plt.xlabel("$\lambda$", fontsize=18)

Text(0.5, 0, '$\\lambda$')

10.2. Epidemic threshold for Barabàsi-Albert model networks

N = 10000
AB = nx.barabasi_albert_graph(N, 10)

nx.is_connected(AB)

True

print(nx.info(AB))

Name: 
Type: Graph
Number of nodes: 10000
Number of edges: 99900
Average degree:  19.9800

sum_k2 = 0
for i in AB.nodes():
    k = AB.degree(i)
    sum_k2 += k * k
avg_k2 = sum_k2 / N
print(avg_k2)

940.6206

avg_deg = 2 * len(AB.edges) / N
print(avg_deg)

19.98

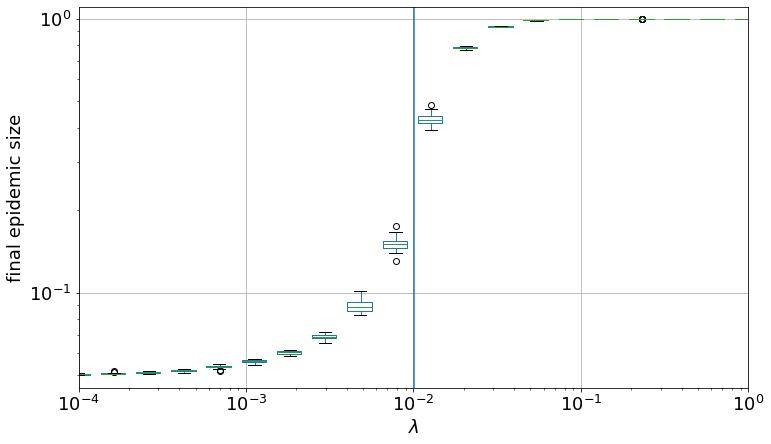
The threshold can be approximated as \(\lambda_c \sim \mu \frac{\langle k \rangle}{\langle k^2 \rangle - \langle k \rangle}\)

lambda_c = mu * avg_deg / (avg_k2 - avg_deg)
print(lambda_c)

0.0043404559824974055

lambda_c / lc

0.43223996856102154

10.2.1. Simulations of an SIR process

We simulate 20 realizations of a SIR model for increasing values of \(\lambda\)

final_size_AB = defaultdict(list)

for lambd in np.geomspace(0.0001, 1.0, 20):
    for r in range(0, 20):

        t, S, I, R = EoN.fast_SIR(AB, lambd, mu, rho=0.05)

        final_size_AB[lambd].append(R[-1] / N)

sf_net_size = pd.DataFrame.from_dict(final_size_AB)

sf_net_size.tail()

	0.000100	0.000162	0.000264	0.000428	0.000695	0.001129	0.001833	0.002976	0.004833	0.007848	0.012743	0.020691	0.033598	0.054556	0.088587	0.143845	0.233572	0.379269	0.615848	1.000000
15	0.0505	0.0507	0.0515	0.0528	0.0533	0.0570	0.0596	0.0824	0.1225	0.2423	0.4803	0.7067	0.8738	0.9585	0.9909	0.9986	0.9999	1.0	1.0	1.0
16	0.0507	0.0507	0.0514	0.0526	0.0539	0.0585	0.0647	0.0796	0.1165	0.2618	0.4837	0.7169	0.8759	0.9585	0.9923	0.9988	0.9998	1.0	1.0	1.0
17	0.0507	0.0506	0.0511	0.0519	0.0541	0.0572	0.0654	0.0877	0.1462	0.2727	0.4790	0.7197	0.8774	0.9599	0.9919	0.9987	0.9996	1.0	1.0	1.0
18	0.0508	0.0505	0.0510	0.0519	0.0539	0.0552	0.0641	0.0813	0.1444	0.2636	0.5012	0.7044	0.8731	0.9540	0.9919	0.9991	1.0000	1.0	1.0	1.0
19	0.0502	0.0510	0.0508	0.0525	0.0537	0.0555	0.0579	0.0779	0.1541	0.2538	0.5092	0.7004	0.8743	0.9579	0.9923	0.9991	0.9996	1.0	1.0	1.0

plt.figure(figsize=(12, 7))

homo_net_size.boxplot(
    positions=np.array(homo_net_size.columns),
    widths=np.array(homo_net_size.columns) / 3,
    color="r",
)

plt.vlines(x=lambda_c, ymin=0.04, ymax=1.1)
sf_net_size.boxplot(
    positions=np.array(sf_net_size.columns), widths=np.array(sf_net_size.columns) / 3
)

plt.yscale("log")
plt.xscale("log")
plt.xlim(0.0001, 1.0)
plt.ylim(0.045, 1.1)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.ylabel("final epidemic size", fontsize=18)
plt.xlabel("$\lambda$", fontsize=18)

Text(0.5, 0, '$\\lambda$')

10.3. Epidemic threshold for configuration model networks

We can use the configuration model to generate a network with a given power-law degree distribution. By setting \(\gamma=2.1\), we expect to see more fluctuations in the degree distribution.

We create a function that samples from a power-law distribution between \(k_{min}\) and \(k_{max}\) with exponent \(\gamma\)

def get_activity(x0, x1, g):

    y = random.uniform(0, 1)

    e = g + 1.0

    a = ((x1**e - x0**e) * y + x0**e) ** (1.0 / e)

    return a

N = 10000
kmin = 2
kmax = N - 1
a = []
for i in range(N):
    act = get_activity(kmin, kmax, -2.1)

    a.append(int(round(act)))

# we need the sum of the degree sequence to be even to properly run the configuration model
if sum(a) % 2 == 0:
    G1 = nx.configuration_model(a)
else:
    a[-1] += 1
    G1 = nx.configuration_model(a)

nx.is_connected(G1)

True

print(nx.info(G1))

Name: 
Type: MultiGraph
Number of nodes: 10000
Number of edges: 65624
Average degree:  13.1248

G1 = nx.Graph(G1)

G1.remove_edges_from(nx.selfloop_edges(G1))

print(nx.info(G1))

Name: 
Type: Graph
Number of nodes: 10000
Number of edges: 54022
Average degree:  10.8044

nx.is_connected(G1)

True

sum_k2 = 0
for i in G1.nodes():
    k = G1.degree(i)
    sum_k2 += k * k
avg_k2 = sum_k2 / N
print(avg_k2)

2428.7296

avg_deg = 2 * len(G1.edges) / N
print(avg_deg)

10.8044

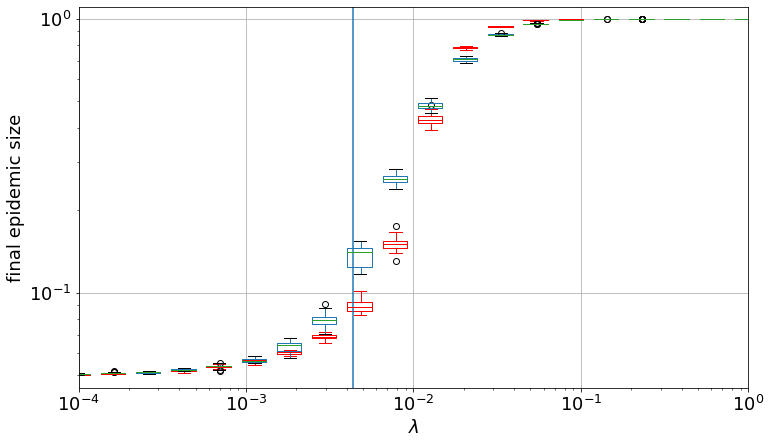
lambda_c1 = mu * avg_deg / (avg_k2 - avg_deg)
print(lambda_c1)

0.000893691831327123

lc / lambda_c1

11.236282381599462

10.3.1. Simulations of an SIR process

We simulate 100 realizations of a SIR model for increasing values of \(\lambda\)

final_size_conf = defaultdict(list)

for lambd in np.geomspace(0.0001, 1.0, 20):
    for r in range(0, 20):

        t, S, I, R = EoN.fast_SIR(G1, lambd, mu, rho=0.05)

        final_size_conf[lambd].append(R[-1] / N)

conf_net_size = pd.DataFrame.from_dict(final_size_conf)

plt.figure(figsize=(12, 7))

boxprops1 = dict(linestyle="-", linewidth=4, color="b")

homo_net_size.boxplot(
    positions=np.array(homo_net_size.columns),
    widths=np.array(homo_net_size.columns) / 3,
)

conf_net_size.boxplot(
    positions=np.array(conf_net_size.columns),
    widths=np.array(conf_net_size.columns) / 3,
    boxprops=boxprops1,
)

plt.vlines(x=lambda_c1, ymin=0.04, ymax=1.1)
plt.legend(["ER", "CM"])
plt.yscale("log")
plt.xscale("log")
plt.xlim(0.0001, 1.0)
plt.ylim(0.045, 1.1)
plt.xticks(fontsize=18)
plt.yticks(fontsize=18)
plt.ylabel("final epidemic size", fontsize=18)
plt.xlabel("$\lambda$", fontsize=18)

Text(0.5, 0, '$\\lambda$')