Basics of network analysis

4. Basics of network analysis#

import networkx as nx
import seaborn as sns

%pylab inline

%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib

4.1. Connectivity and clustering of a graph#

We study the network of coauthorships of Astro-Ph, from the SNAP database.

filepath = "./../datasets/ca-AstroPh.txt"

!more ./../datasets/cma-AstroPh.txt

./../datasets/cma-AstroPh.txt: No such file or directory

G = nx.Graph()

fh = open(filepath, "r")
for line in fh.readlines():
    s = line.strip().split()
    if s[0] != "#":
        origin = int(s[0])
        dest = int(s[1])
        G.add_edge(origin, dest)
fh.close()

print("The graph has", len(G), "nodes and", len(G.edges()), "edges")

The graph has 18772 nodes and 198110 edges

<networkx.classes.graph.Graph at 0x158bfc160>

print("Is the graph simply connected?", nx.is_connected(G))

Is the graph simply connected? False

4.1.1. Show the components of the graph#

print("The graph has", nx.number_connected_components(G), "connected components")

The graph has 290 connected components

for k in nx.connected_components(G):
    print(len(k))

4.1.2. Extract the largest Connected Component as a subgraph#

nx.connected_components(G)

<generator object connected_components at 0x158be69e0>

graphs = list(nx.connected_components(G))

H = G.subgraph(graphs[0])

len(H)

print(len(G) - len(H))

print("Check that the graph is now connected")
nx.is_connected(H)

Check that the graph is now connected

True

4.2. Global clustering coefficient#

The global clustering coefficient measures the number of triangles in the network and it’s defined as:

$C_\Delta = \frac{3 \times \text{triangles}}{\text{triplets}}$

nx.triangles(H)

{84424: 210,
54,
218,
1,
918,
107,
820,
137,
828,
3,
44,
13,
1906,
3,
11,
506,
128,
2759,
16,
1793,
487,
2384,
189,
702,
27,
5646,
148,
360,
44,
1594,
1,
23,
10,
10,
158,
354,
934,
76,
1587,
73,
101,
11,
537,
205,
423,
8,
396,
1145,
236,
15,
6,
117,
72,
121,
236,
32,
143,
513,
113,
11,
285,
114,
32,
491,
3003,
 104802: 1907,
 106611: 526,
 107829: 412,
 109016: 29,
 112605: 623,
 117751: 41,
 122908: 295,
 124023: 89,
 125190: 1,
 130825: 42,
 132445: 1246,
3,
50,
1001,
1,
142,
1,
90,
110,
22,
780,
650,
68,
29,
49,
41,
1409,
 112293: 84,
 113138: 1104,
 116343: 45,
 116453: 104,
 118859: 233,
 121831: 111,
 122003: 5,
 123268: 28,
 125345: 172,
 127886: 5187,
 129530: 187,
 129910: 45,
 132104: 57,
9,
1081,
7,
41,
3028,
46,
378,
4324,
73,
12,
1930,
6157,
969,
58,
4399,
486,
5,
13,
6711,
71,
5282,
0,
1102,
11,
1248,
122,
2251,
2318,
0,
30,
1201,
462,
108,
17,
1000,
79,
378,
1429,
4,
543,
147,
555,
4975,
1377,
20,
14,
195,
999,
548,
386,
1590,
18,
629,
187,
642,
0,
1003,
130,
7,
6826,
2152,
 101953: 196,
 105827: 110,
 110499: 23,
 112243: 0,
 115344: 35,
 118103: 1133,
 118630: 382,
 118958: 51,
 120454: 400,
 126152: 81,
 130165: 380,
42,
1,
28,
41,
0,
11,
15,
76,
18,
19,
166,
5,
1,
1052,
10,
7,
3,
15,
 104589: 479,
 106833: 85,
 110210: 430,
 113335: 15,
 118286: 10,
 120586: 32,
 121399: 1832,
 121988: 68,
 122460: 18,
 127393: 216,
11,
142,
376,
8,
132,
1541,
599,
1369,
193,
1954,
2,
685,
131,
3,
586,
59,
120,
2256,
516,
154,
106,
28,
82,
853,
58,
2,
409,
357,
8,
429,
1762,
1405,
23,
822,
 100099: 1666,
 102617: 1939,
 106954: 21,
 107534: 671,
 107797: 320,
 107933: 260,
 112779: 206,
 112903: 22,
 115420: 205,
 117953: 875,
 123695: 62,
 124913: 238,
 131639: 55,
 132766: 2,
 106274: 3070,
490,
3006,
1880,
36,
4132,
33,
888,
422,
859,
231,
859,
846,
1922,
2055,
1493,
269,
410,
922,
1637,
506,
351,
921,
1068,
36,
196,
610,
36,
1927,
948,
554,
8186,
843,
171,
683,
2529,
1769,
1460,
1489,
22,
496,
535,
473,
36,
635,
7065,
91,
153,
1067,
1007,
9008,
447,
4793,
2308,
289,
207,
1005,
899,
1820,
1835,
36,
1441,
198,
1119,
582,
902,
601,
1164,
253,
740,
4197,
362,
11269,
363,
919,
1880,
104,
844,
893,
2212,
25,
834,
540,
3315,
252,
1894,
2270,
676,
839,
1401,
109,
402,
153,
926,
2223,
1521,
2673,
1537,
1105,
193,
579,
346,
499,
964,
777,
2003,
4490,
1995,
829,
1322,
407,
1213,
1200,
380,
2154,
35,
2947,
28,
1330,
462,
89,
1835,
2134,
 100394: 2275,
 100461: 867,
 100717: 820,
 102653: 621,
 103169: 1306,
 104241: 598,
 105680: 3343,
 106763: 1432,
 107846: 1397,
 108722: 302,
 109056: 253,
 111385: 1950,
 111660: 1041,
 111709: 2061,
 112157: 2382,
 112695: 1113,
 112848: 1861,
 113726: 858,
 113825: 671,
 114249: 954,
 115209: 3395,
 115281: 206,
 115607: 3644,
 115700: 307,
 116194: 21,
 116337: 1529,
 118896: 779,
 119042: 36,
 119664: 1682,
 120199: 1889,
 120618: 2541,
 121461: 465,
 122425: 1180,
 122495: 827,
 123233: 485,
 125226: 871,
 125267: 824,
 125557: 338,
 125678: 1090,
 125766: 77,
 125774: 312,
 126948: 643,
 127225: 259,
 127274: 455,
 127816: 670,
 129273: 1271,
 129410: 899,
 129483: 509,
 131234: 940,
 131592: 820,
28,
332,
36,
1654,
56,
117,
17,
42,
853,
284,
180,
362,
117,
1291,
397,
152,
464,
184,
1512,
116,
54,
540,
100,
179,
2594,
195,
6,
 101422: 47,
 105901: 710,
 106176: 425,
 107608: 197,
 108944: 189,
 111957: 723,
 112410: 37,
 119031: 529,
 119480: 412,
 121026: 1868,
 124998: 106,
 125365: 696,
 128934: 36,
 131519: 77,
 131914: 94,
 132206: 646,
276,
276,
525,
38,
78,
47,
431,
870,
446,
81,
79,
145,
78,
3468,
279,
82,
78,
88,
78,
206,
282,
679,
168,
286,
140,
320,
518,
15,
727,
297,
276,
327,
6,
373,
 101326: 4,
 101994: 780,
 112383: 285,
 115063: 276,
 117676: 442,
 118912: 875,
 121209: 91,
 128878: 276,
 131320: 489,
0,
4,
0,
7,
3,
1,
6,
1,
11,
0,
 119665: 1,
 122165: 1,
 122336: 1,
 130188: 1,
5,
30,
1,
23,
635,
3,
0,
 103432: 1,
 109229: 180,
 122293: 1,
 130391: 195,
3,
502,
531,
22,
1,
8,
23,
58,
3,
843,
3,
214,
 116725: 3,
 116919: 13,
184,
264,
283,
239,
153,
153,
490,
153,
8,
153,
11,
3,
471,
477,
6,
3,
163,
169,
1034,
 110812: 235,
 111014: 175,
 111916: 7,
 117311: 6,
 122105: 159,
 122740: 197,
 124653: 166,
 130921: 24,
821,
212,
618,
1331,
353,
941,
436,
373,
573,
257,
1331,
728,
564,
547,
522,
529,
527,
1220,
19,
1767,
656,
285,
1177,
171,
637,
1198,
698,
21,
22,
560,
869,
736,
668,
59,
530,
329,
708,
673,
1348,
364,
519,
1334,
234,
140,
954,
652,
200,
787,
368,
671,
606,
 100548: 523,
 104544: 913,
 105528: 929,
 105725: 42,
 107436: 1048,
 110773: 75,
 114530: 1984,
 120321: 650,
 123670: 1027,
 131704: 1718,
 133062: 970,
3,
1,
12,
3,
30,
 108170: 22,
 112976: 2,
34,
17,
87,
9,
33,
42,
211,
 123201: 41,
3,
14,
0,
 110535: 3,
55,
3,
21,
6,
10,
2421,
81,
27,
6,
2,
9,
39,
14,
61,
2,
1,
1,
14,
3,
1,
40,
1,
6,
8,
284,
4,
3,
125,
3,
2,
122,
3,
1,
3,
2,
5,
27,
1,
69,
5,
23,
111,
 100536: 39,
 109585: 2,
 109894: 63,
 112256: 12,
 120094: 3,
 120169: 4,
 127688: 4,
 131741: 4,
 132492: 1480,
 132691: 2,
2,
4,
3,
3,
27,
4,
1,
3,
3,
15,
 113717: 8,
 119757: 4,
 123558: 3,
 118675: 36,
139,
702,
17,
214,
67,
18,
150,
18,
13,
79,
19,
115,
17,
 105955: 40,
 113867: 39,
 125136: 61,
35,
7,
97,
3,
2776,
27,
56,
13,
19,
327,
1006,
0,
3,
11,
48,
 101610: 166,
 107618: 25,
 109192: 17,
 114995: 0,
 120732: 167,
 122852: 91,
 128685: 1229,
196,
107,
1329,
21,
1600,
69,
1,
3,
23,
1525,
8,
4,
271,
1487,
1746,
26,
4,
6,
1406,
3,
30,
21,
2,
236,
21,
28,
4,
39,
1095,
108,
32,
 101271: 21,
 102475: 0,
 102874: 95,
 104466: 6,
 106392: 152,
 110670: 109,
 111496: 2053,
 114677: 1350,
 128657: 230,
 128732: 1095,
 129683: 908,
 130919: 36,
108,
16,
784,
29,
28,
1065,
77,
27,
308,
0,
78,
32,
 118945: 14,
46,
91,
 126260: 1,
781,
1771,
2355,
1988,
3053,
1,
325,
366,
331,
524,
28,
1267,
3544,
55,
353,
3834,
69,
1806,
2231,
2206,
748,
222,
906,
490,
3361,
581,
5103,
360,
3936,
3,
1997,
314,
1018,
3,
4088,
1487,
3067,
3423,
605,
573,
175,
1845,
55,
3538,
619,
2092,
144,
190,
18,
 100181: 580,
 100237: 156,
 101520: 445,
 105651: 296,
 108958: 609,
 111161: 6457,
 112453: 375,
 113591: 1093,
 117816: 26,
 121653: 51,
 121655: 15,
 124529: 2813,
 126451: 868,
 126916: 3154,
 128381: 325,
 128985: 36,
 129458: 595,
 130997: 5373,
2522,
3217,
484,
1540,
3330,
3232,
1555,
231,
370,
1614,
3755,
3115,
3856,
190,
360,
1276,
5596,
2289,
1002,
527,
442,
171,
409,
2580,
1492,
1386,
791,
1471,
1524,
4185,
992,
1416,
2257,
1533,
1529,
511,
2369,
1976,
3365,
549,
1408,
1149,
3163,
1550,
687,
2516,
1516,
2531,
4234,
3683,
218,
1030,
2980,
1684,
1540,
379,
1540,
1276,
409,
933,
3944,
253,
967,
1540,
2300,
3857,
6515,
441,
3383,
171,
436,
1542,
0,
4834,
1667,
1794,
1036,
8357,
1515,
3312,
979,
4756,
3357,
1868,
105,
1579,
1804,
 100621: 3,
 100930: 1373,
 101167: 3414,
 101641: 312,
 102282: 414,
 103290: 714,
 104749: 2372,
 105049: 2917,
 106945: 1057,
 107877: 3566,
 110402: 1379,
 114352: 2914,
 115480: 3788,
 115796: 153,
 115900: 4620,
 119515: 3029,
 122753: 190,
 122787: 3086,
 125954: 2915,
 126258: 85,
 128641: 1004,
 130519: 2973,
 130853: 2973,
 131221: 2488,
 ...}

How many triangles are there in the whole network?

tt = sum(list(nx.triangles(H).values()))

tt / 3

1350014.0

The transitivity is the fraction of all possible triangles in the network.

4.3. Average clustering coefficient#

As an alternative to the global clustering coefficient, the overall level of clustering in a network is measured by Watts and Strogatz as the average of the local clustering coefficients of all the vertices $n$:

$\bar{C} = \frac{1}{n}\sum_{i=1}^{n} C_i.$

It is worth noting that this metric places more weight on the low degree nodes, while the transitivity ratio places more weight on the high degree nodes. In fact, a weighted average where each local clustering score is weighted by $k_i(k_i-1)$ is identical to the global clustering coefficient.

print("The average clustering coefficient of H is")
nx.average_clustering(H)

The average clustering coefficient of H is

0.6328232091518589

4.4. Average sorthest path length#

4.4.1. Warning! Calculating the shortest paths is intensive!!#

The graph is small world.

nx.average_shortest_path_length(H)

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In [22], line 1
----> 1 nx.average_shortest_path_length(H)

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/algorithms/shortest_paths/generic.py:417, in average_shortest_path_length(G, weight, method)
    413         return nx.single_source_bellman_ford_path_length(G, v, weight=weight)
    415 if method in single_source_methods:
    416     # Sum the distances for each (ordered) pair of source and target node.
--> 417     s = sum(l for u in G for l in path_length(u).values())
    418 else:
    419     if method == "floyd-warshall":

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/algorithms/shortest_paths/generic.py:417, in <genexpr>(.0)
    413         return nx.single_source_bellman_ford_path_length(G, v, weight=weight)
    415 if method in single_source_methods:
    416     # Sum the distances for each (ordered) pair of source and target node.
--> 417     s = sum(l for u in G for l in path_length(u).values())
    418 else:
    419     if method == "floyd-warshall":

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/algorithms/shortest_paths/generic.py:409, in average_shortest_path_length.<locals>.path_length(v)
    407 def path_length(v):
    408     if method == "unweighted":
--> 409         return nx.single_source_shortest_path_length(G, v)
    410     elif method == "dijkstra":
    411         return nx.single_source_dijkstra_path_length(G, v, weight=weight)

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/algorithms/shortest_paths/unweighted.py:59, in single_source_shortest_path_length(G, source, cutoff)
     57     cutoff = float("inf")
     58 nextlevel = {source: 1}
---> 59 return dict(_single_shortest_path_length(G.adj, nextlevel, cutoff))

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/algorithms/shortest_paths/unweighted.py:91, in _single_shortest_path_length(adj, firstlevel, cutoff)
     89         return
     90     for v in found:
---> 91         nextlevel.update(adj[v])
     92     level += 1
     93 del seen

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/classes/coreviews.py:282, in <genexpr>(.0)
    280 if node_ok_shorter:
    281     return (n for n in self.NODE_OK.nodes if n in self._atlas)
--> 282 return (n for n in self._atlas if self.NODE_OK(n))

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/classes/coreviews.py:337, in FilterAdjacency.__getitem__.<locals>.new_node_ok(nbr)
    336 def new_node_ok(nbr):
--> 337     return self.NODE_OK(nbr) and self.EDGE_OK(node, nbr)

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/classes/filters.py:20, in no_filter(*items)
      1 """Filter factories to hide or show sets of nodes and edges.
      2 
      3 These filters return the function used when creating `SubGraph`.
      4 """
      5 __all__ = [
      6     "no_filter",
      7     "hide_nodes",
   (...)
     16     "show_multidiedges",
     17 ]
---> 20 def no_filter(*items):
     21     return True
     24 def hide_nodes(nodes):

KeyboardInterrupt: 

math.log(len(H), 10)

4.4.2. Compare the results with a random ER network#

We generate a random Erdos-Renyi graph with same average connectivity of H, i.e. same number of nodes and edges.

nnodes = 2000
plink = 0.0122

ER = nx.fast_gnp_random_graph(nnodes, plink)

nx.is_connected(ER)

True

print("The ER graph has", len(ER), "nodes")
print("and", len(ER.edges()), "edges")

The ER graph has 2000 nodes
and 24467 edges

print("The average clustering coefficient of ER is")
nx.average_clustering(ER)

The average clustering coefficient of ER is

0.011958816979123639

print(sum(list(nx.triangles(ER).values())) / 3)

2370.0

The ER graph is also small world!

The average shortest path scales approximately with the logarithm of the number of nodes

nx.average_shortest_path_length(ER)

math.log(len(ER), 10)

4.4.3. Compare the results with a random AB network#

AB = nx.barabasi_albert_graph(18000, 11)

print("The AB graph has", len(AB), "nodes")
print("and", len(AB.edges()), "edges")

The AB graph has 18000 nodes
and 197879 edges

from collections import Counter

degrees = dict(AB.degree()).values()
c = Counter(degrees)

import powerlaw as pwl

plt.figure(figsize=(10, 7))
x = []
y = []
for i in sorted(c):
    x.append(i)
    y.append(float(c[i]) / len(AB))


plt.plot(np.array(x), np.array(y))
pwl.plot_pdf(list(degrees))

plt.xlabel("$k$", fontsize=18)
plt.ylabel("$P(k)$", fontsize=18)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.yscale("log")
plt.xscale("log")
plt.axis([10, 1000, 0.0000001, 1])
plt.show()

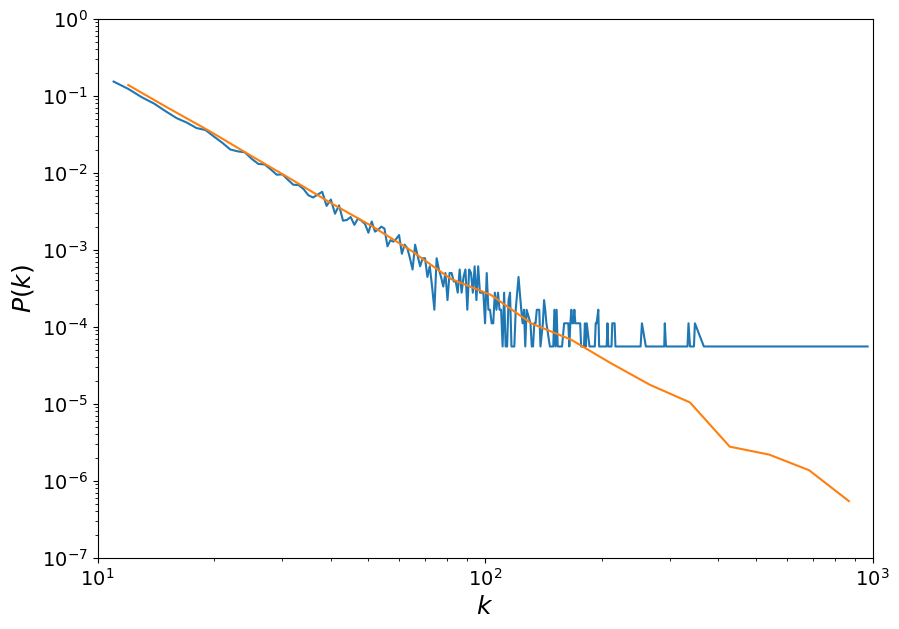
../_images/c7c90e4fefbfbc85fe675fe85ff91f9eaf9abe073c6171cce70c778dd4f6f37d.png

fit_function = pwl.Fit(list(degrees), xmin=11)

fit_function.power_law.alpha

3.05323051233271

fit_function.power_law.sigma

0.015303876663508869

fit_function.power_law.xmin

11.0

print("The average clustering coefficient of AB is")
nx.average_clustering(AB)

The average clustering coefficient of AB is

0.007877683345432804

print("The number of triangles is ", sum(list(nx.triangles(AB).values())) / 3)

The number of triangles is  24257.0

The AB network is also small-world.

nx.average_shortest_path_length(AB)

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In [39], line 1
----> 1 nx.average_shortest_path_length(AB)

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/algorithms/shortest_paths/generic.py:417, in average_shortest_path_length(G, weight, method)
    413         return nx.single_source_bellman_ford_path_length(G, v, weight=weight)
    415 if method in single_source_methods:
    416     # Sum the distances for each (ordered) pair of source and target node.
--> 417     s = sum(l for u in G for l in path_length(u).values())
    418 else:
    419     if method == "floyd-warshall":

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/algorithms/shortest_paths/generic.py:417, in <genexpr>(.0)
    413         return nx.single_source_bellman_ford_path_length(G, v, weight=weight)
    415 if method in single_source_methods:
    416     # Sum the distances for each (ordered) pair of source and target node.
--> 417     s = sum(l for u in G for l in path_length(u).values())
    418 else:
    419     if method == "floyd-warshall":

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/algorithms/shortest_paths/generic.py:409, in average_shortest_path_length.<locals>.path_length(v)
    407 def path_length(v):
    408     if method == "unweighted":
--> 409         return nx.single_source_shortest_path_length(G, v)
    410     elif method == "dijkstra":
    411         return nx.single_source_dijkstra_path_length(G, v, weight=weight)

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/algorithms/shortest_paths/unweighted.py:59, in single_source_shortest_path_length(G, source, cutoff)
     57     cutoff = float("inf")
     58 nextlevel = {source: 1}
---> 59 return dict(_single_shortest_path_length(G.adj, nextlevel, cutoff))

File ~/.pyenv/versions/venv_xgi/lib/python3.9/site-packages/networkx/algorithms/shortest_paths/unweighted.py:91, in _single_shortest_path_length(adj, firstlevel, cutoff)
     89         return
     90     for v in found:
---> 91         nextlevel.update(adj[v])
     92     level += 1
     93 del seen

KeyboardInterrupt: 

math.log(len(AB), 10)

4.4.4. Compare the results with a random WS network#

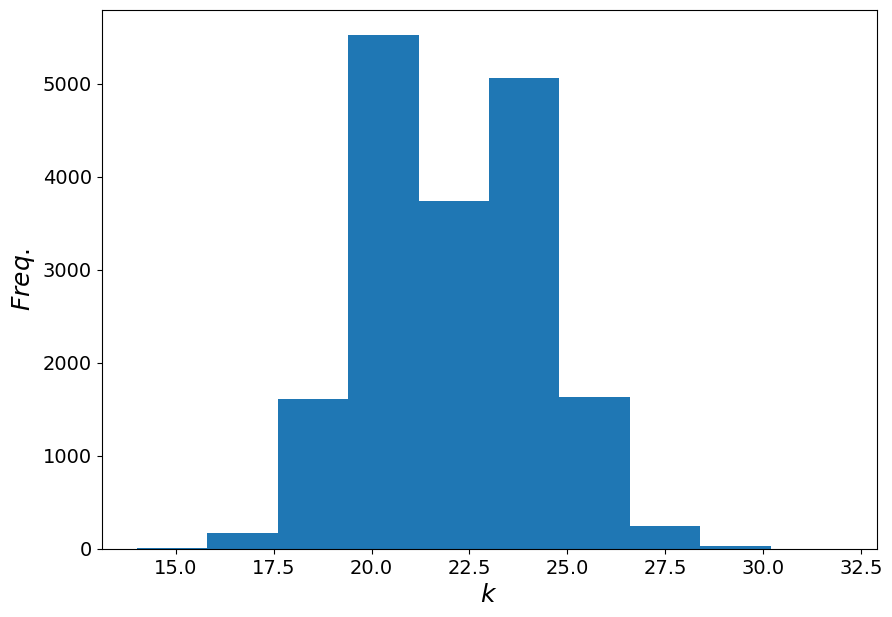
WS = nx.connected_watts_strogatz_graph(18000, 23, 0.2, 50)

print("The WS graph has", len(WS), "nodes")
print("and", len(WS.edges()), "edges")

The WS graph has 18000 nodes
and 198000 edges

nx.is_connected(WS)

True

ws_degrees = dict(WS.degree()).values()

plt.figure(figsize=(10, 7))
plt.hist(ws_degrees, bins=10)
plt.xlabel("$k$", fontsize=18)
plt.ylabel("$Freq.$", fontsize=18)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)

(array([   0., 1000., 2000., 3000., 4000., 5000., 6000.]),
 [Text(0, 0.0, '0'),
  Text(0, 1000.0, '1000'),
  Text(0, 2000.0, '2000'),
  Text(0, 3000.0, '3000'),
  Text(0, 4000.0, '4000'),
  Text(0, 5000.0, '5000'),
  Text(0, 6000.0, '6000')])

../_images/9777f1153cfd1d5cdc29529f6084c4084e97e2c7f7f66a576b6f70479d195ab0.png

print("The average clustering coefficient of WS is")
nx.average_clustering(WS)

The average clustering coefficient of WS is

0.3675862599323307

The Watt-Strogatz network is still small-world but with high clustering.

nx.average_shortest_path_length(WS)

math.log(len(WS), 10)

4.5. Closeness Centrality#

In connected graphs there is a natural distance metric between all pairs of nodes, defined by the length of their shortest paths. The ‘’’farness’’’ of a node ‘’x’’ is defined as the sum of its distances from all other nodes, and its closeness was defined by Bavelas as the reciprocal of the farness that is:

$C(x)= \frac{1}{\sum_y d(y,x)}.$

Thus, the more central a node is the lower its total distance from all other nodes. Note that taking distances ‘’from’’ or ‘’to’’ all other nodes is irrelevant in undirected graphs, whereas in directed graphs distances ‘’to’’ a node are considered a more meaningful measure of centrality, as in general (e.g., in, the web) a node has little control over its incoming links.

Be careful! Computing all the distances between pair of nodes can be intensive.

close_centr = nx.closeness_centrality(H, 84424)

print(close_centr)