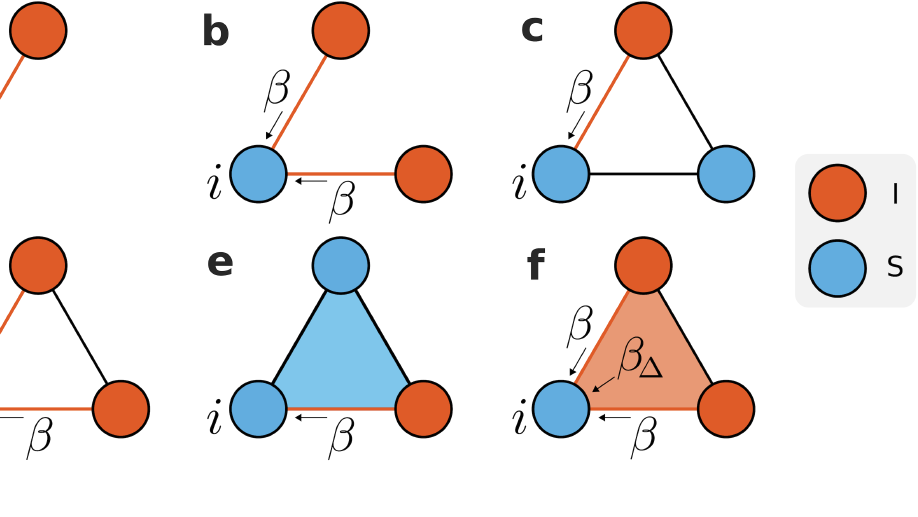
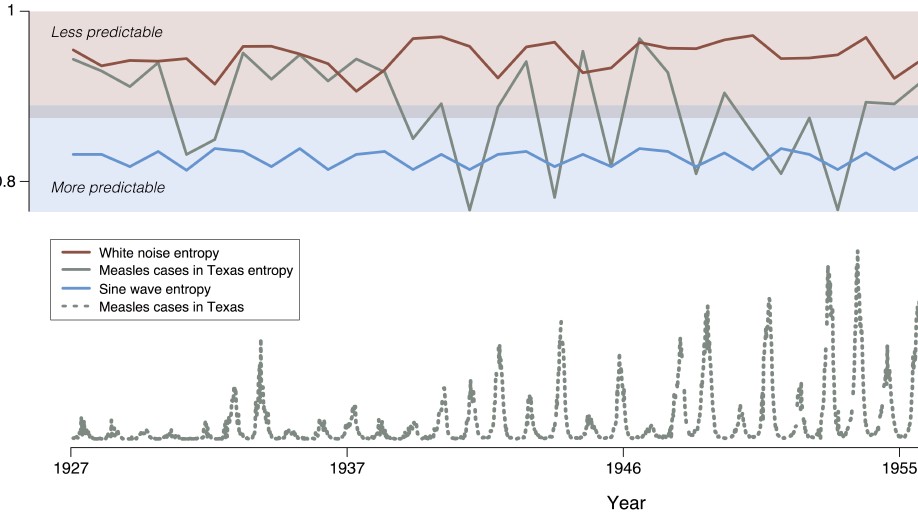
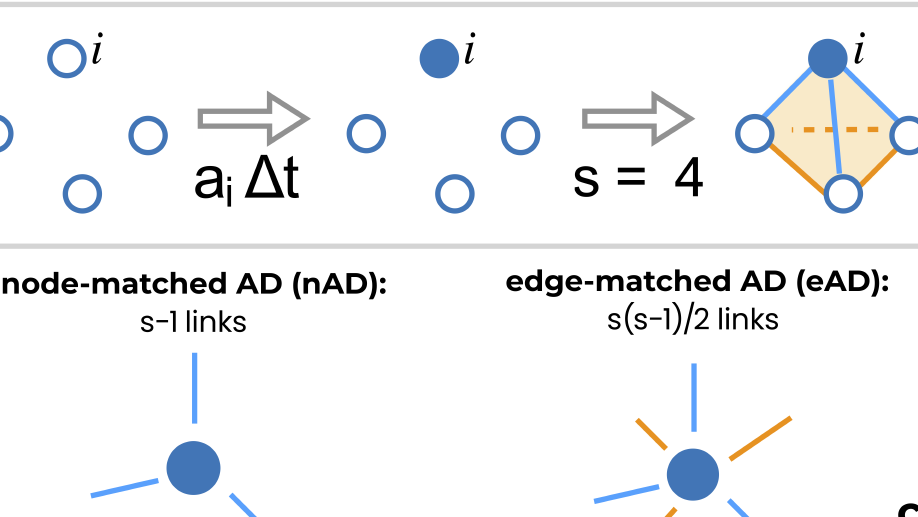
Biography
I am a Professor in the Network Science Institute at Northeastern University London.
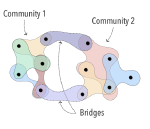
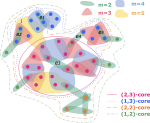
My main research focus is on the theoretical and empirical analysis of complex systems, with an emphasis on the structural and temporal properties of networks with higher‐order interactions and feedback dynamics.
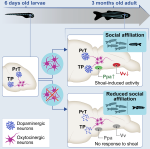
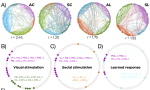
I have broadened my research to include social contagion and team dynamics, the investigation of whole‐brain activation patterns, and the structure of cognitive representations in natural and syntethic neural architectures, with particular reference to their topological structure, merging statistical physics approach, algebraic topology and data analysis.
My current topics of interests are:
i) extending models of cooperating behavioural and biological spreading processes with explicit group interactions with the aim to link them to socio‐economical data;
ii) the dynamical connectivity during resting state and tasks, aiming to build robust quantitative tools to be used as building blocks to develop biomarkers and as guiding principles to reverse‐engineer functional connectivity dynamics, with the ultimate aim of linking them to higher cognitive functions, e.g. control and decision making.
Academic affiliations: Principal Researcher at CENTAI, Guest Scholar Networks Units IMT Lucca.
Previous: ISI Foundation, Imperial College London
Interests
- Topology and Predictability of Complex Systems
- Computational Neuroscience
- Cognitive Control
Education
-
PhD in Complex Networks, 2012
Imperial College London
-
MSc in Theoretical Physics, 2008
University of Pisa
-
BSc in Physics, 2005
University of Pisa