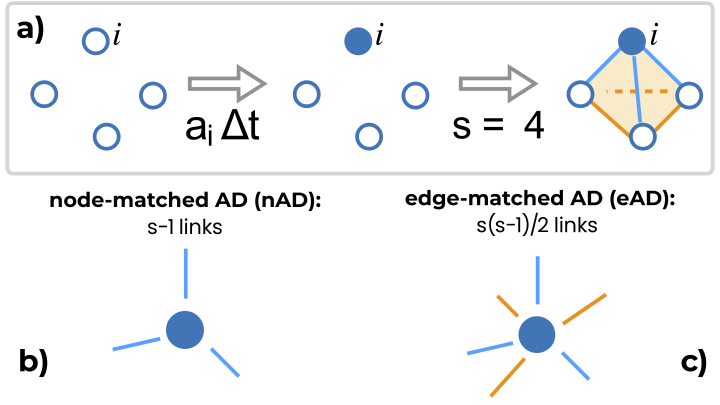
Abstract
Many complex systems find a convenient representation in terms of networks: structures made by pairwise interactions (links) of elements (nodes). For many biological and social systems, elementary interactions involve however more than two elements, and simplicial complexes are more adequate to describe such phenomena. Moreover, these interactions often change over time. Here, we propose a framework to model such an evolution: the Simplicial Activity Driven (SAD) model, in which the building block is a simplex of nodes representing a multi-agent interaction. We show analytically and numerically that the use of simplicial structures leads to crucial differences in the outcome of paradigmatic processes modelling disease propagation or social contagion, with respect to the activity-driven (AD) model, a paradigmatic temporal network model involving only binary interactions. In particular, fluctuations in the number of nodes involved in the interactions can affect the outcome of models of simple contagion processes, contrarily to what happens in the AD model. Moreover, social contagion models such as cascading processes present a much richer phenomenology and can become extremely slow when occurring on evolving simplicial complexes.