On the predictability of infectious disease outbreaks

Abstract

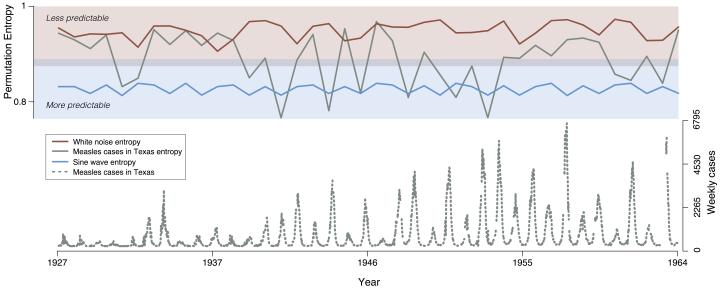
Infectious disease outbreaks recapitulate biology: they emerge from the multi-level interaction of hosts, pathogens, and their shared environment. As a result, predicting when, where, and how far diseases will spread requires a complex systems approach to modeling. Recent studies have demonstrated that predicting different components of outbreaks–e.g., the expected number of cases, pace and tempo of cases needing treatment, importation probability etc.–is feasible. Therefore, advancing both the science and practice of disease forecasting now requires testing for the presence of fundamental limits to outbreak prediction. To investigate the question of outbreak prediction, we study the information theoretic limits to forecasting across a broad set of infectious diseases using permutation entropy as a model independent measure of predictability. Studying the predictability of a diverse collection of historical outbreaks–including, gonorrhea, influenza, Zika, measles, polio, whooping cough, and mumps–we identify a fundamental entropy barrier for time series forecasting. However, we find that for most diseases this barrier to prediction is often well beyond the time scale of single outbreaks, implying prediction is likely to succeed. We also find that the forecast horizon varies by disease and demonstrate that both shifting model structures and social network heterogeneity are the most likely mechanisms for the observed differences in predictability across contagions. Our results highlight the importance of moving beyond time series forecasting, by embracing dynamic modeling approaches to prediction and suggest challenges for performing model selection across long disease time series. We further anticipate that our findings will contribute to the rapidly growing field of epidemiological forecasting and may relate more broadly to the predictability of complex adaptive systems.