Multistability, intermittency and hybrid transitions in social contagion models on hypergraphs
Abstract
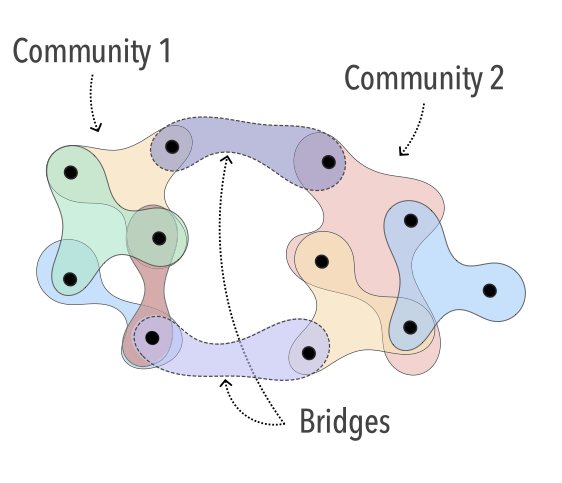
Although ubiquitous, interactions of groups of individuals (e.g., modern messaging applications, group meetings, or even a parliament discussion) are not yet thoroughly studied. Frequently, single-groups are modeled as critical-mass dynamics, which is a widespread concept used not only by academics but also by politicians and the media. However, less explored questions are how a collection of groups will behave and how the intersection between these groups might change the global dynamics. Here, we formulate this process in terms of binary state dynamics on hypergraphs. We showed that our model has a very rich and unexpected behavior that goes beyond discontinuous transitions. In particular, we might have multistability and intermittency as a consequence of bimodal state distributions. By using artificial random models, we demonstrated that this phenomenology could be associated with community structures. Specifically, we might have multistability or intermittency by controlling the number of bridges between two communities with different densities. The introduction of bridges destroys multistability but creates an intermittent behavior. Furthermore, we provide an analytical formulation showing that the observed pattern for the order parameter and susceptibility are compatible with hybrid phase transitions. Our findings open new paths for research, ranging from physics, on the formal calculation of quantities of interest, to social sciences, where new experiments can be designed.