Connecting Hodge and Sakaguchi-Kuramoto: a mathematical framework for coupled oscillators on simplicial complexes

Abstract

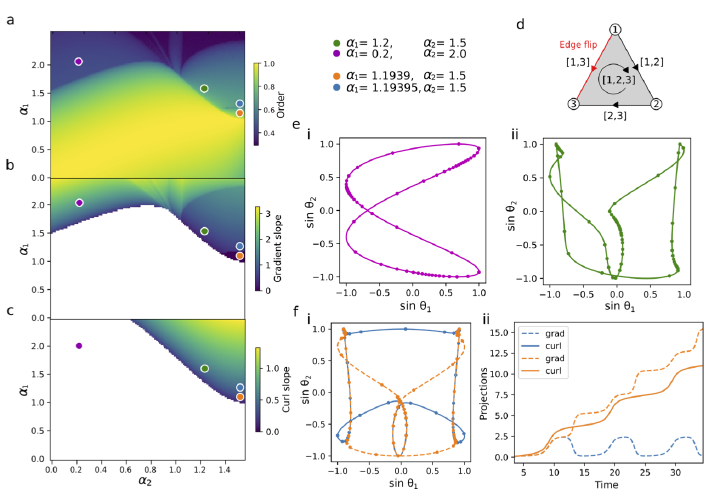
We formulate a general Kuramoto model on weighted simplicial complexes where phases oscillators are supported on simplices of any order k. Crucially, we introduce linear and non-linear frustration terms that are independent of the orientation of the k+1 simplices, providing a natural generalization of the Sakaguchi-Kuramoto model. In turn, this provides a generalized formulation of the Kuramoto higher-order parameter as a potential function to write the dynamics as a gradient flow. We study the properties of the dynamics of the simplicial Sakaguchi-Kuramoto model with oscillators on edges using a selection of simplicial complexes of increasingly complex structure, to highlight the complexity of dynamical behaviors emerging from even simple simplicial complexes. In particular, using the Hodge decomposition of the solution, we understand how the nonlinear frustration couples the dynamics in orthogonal subspaces. We discover various dynamical phenomena, such as the partial loss of synchronization in subspaces aligned with the Hodge subspaces and the emergence of simplicial phase re-locking in regimes of high frustration.